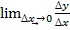Как доказать что последовательность фундаментальна

Критерий Коши сходимости последовательности.

Фундаментальная последовательность.

Последовательность \(\\>\) называют фундаментальной, если она удовлетворяет условию Коши: для каждого \(\varepsilon>0\) существует такое натуральное число \(n_<\varepsilon>\), что для любого \(n\geq n_<\varepsilon>\) и любого \(m\geq n_<\varepsilon>\) справедливо неравенство \(|x_-x_| 0 \ \exists n_<\varepsilon>: \ \forall n\geq n_ <\varepsilon>\ \forall m\geq n_<\varepsilon>\rightarrow|x_-x_| 0 \ \exists n_<\varepsilon>: \ \forall n\geq n_ <\varepsilon>\ \forall p\in\mathbb\rightarrow|x_-x_| Теорема.

Для того чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она была фундаментальной.

Необходимость. Пусть последовательность \(\\>\) имеет конечный предел, равный a. По определению предела
$$
\forall\varepsilon>0 \displaystyle \exists N_<\varepsilon>:\forall p\geq N_<\varepsilon>\rightarrow|x_

-a| 0 \ \exists n_\varepsilon:\forall n\geq n_\varepsilon \ \forall m\geq n_\varepsilon\rightarrow|x_n-x_m| 0 \ \exists k_\varepsilon:\quad \forall k\geq k_\varepsilon\rightarrow Пример.

Доказать, что последовательность \(\\), где
$$
x_=1+\frac<1><2>+\ldots+\frac<1>,\nonumber
$$
расходится.

\(\triangle\) Последовательность \(\\>\) расходится, если не выполняется условие Коши \eqref, то есть
$$
\exists \varepsilon_0>0: \ \forall k\in\mathbb\quad\exists n\geq k\quad\exists m\geq k: \ |x_-x_|\geq \varepsilon_0.\label
$$

Таким образом, условие \eqref выполняется при \(\displaystyle \varepsilon_0=\frac<1><2>\), и в силу критерия Коши последовательность \(\\>\) расходится. \(\blacktriangle\)

Источник

Как первокурсник определение Коши сократил

Под катом я расскажу Вам маленькую и отнюдь не шокирующую историю, большинство из вас, наверное, скажет что я надумал хоть какую-то важность этого события и что все нижеописанное является очевидным, но для меня это было маленькой победой. Если все же интересно, добро пожаловать.

Сразу хочется обговорить несколько моментов: я первокурсник, поэтому в матанализе я смысле ровном счетом ничего, ни на какое открытие не претендую и статью написал, чтобы послушать мнение местных экспертов.

Все началось с первого в моей жизни коллоквиума по дисциплине Математический анализ, одно из заданий которого содержало определение не фундаментальной последовательности по Коши. Под катом трафик.
Я, не долго думая, написал следущее:

Посмотрел, прикинул и оставил. Через неделю получил свою работу с не зачтенным номером с кратким пояснением.

Меня это расстроило, и я решил понять, действительно ли мой вариант неправилен, решил подойти к преподавателю. После долгих дискуссий и формальных объяснений я попросил привести мне контр-пример, на что получил согласие, однако учитель обмолвился, что ему требуется время и что даже если мы не можем придумать такой пример не значит, что его нет.

Спустя пару преподаватель подозвал меня, чтобы доказать мне контр-примером то, что мое определение является лишь частным случаем. На тот момент я уже и сам склонялся к этому, однако решил выслушать. После того, как он расписал огромную и сложную последовательность, которую ваш покорный слуга, увы, забыл, он начал уже было объяснять мне и тут я понимаю, что этот пример более чем полностью удовлетворяет моему определению не фундаментальной последовательности. Уже на этом этапе моя оценка была исправлена на 5, с обмолвкой о том, что преподаватель все же убежден, что формально я не прав. Однако об оценке уже никто не думал, целую неделю я провел в размышлениях о контр-примере для моего определения.

Спустя неделю, так ни к чему и не придя, подошел я к преподавателю и рассказав о том, что я потерпел крах в поиске анти-примера, услышал, что по мнению преподавателя оба утверждения эквивалентны.
Вот доказательство, которое мы соорудили:
Доказывать будем эквивалентность утверждений фундаментальности. Возьмем отрицание от моего определения не фундаментальной последовательности.

И рассмотрим два следования, чтобы доказать эквивалентность.

Таким образом, из определения Коши можно убрать к-нулевое. Хотелось бы получить фидбек, особенно на предмет правильности доказательства.

Источник

Б1. 35. Фундаментальная последовательность

Фундаментальная последовательность (последовательность Коши, сходящаяся в себе последовательность) – последовательность<x_n>, удовлетворяющая следующему условию Коши:

Для любого ε > 0 существует такое n, что для всех n > N, m > N выполняется неравенство |x_n – x_m|

· Пополнение метрического пространства единственно, с точностью до изометрии.

· Полнота наследует замкнутыми подмножествами полного метрического пространства.

· Метрическое пространство компактно тогда и только тогда, когда оно полно и вполне ограничено, то есть для любого пространство можно покрыть конечным числом шаром радиуса

· Топологическим свойством является наличие хотя бы одной полной метрики в классе метрик, порождающих топологию метрического пространства

· Множество вещественных чисел полно в стандартной метрике

· Вообще, любое конечномерное евклидово или унитарное пространство полно

· Свойство полноты является обязательным в определении банахова пространства, в частности гильбертова пространства.

· Пространство непрерывных на отрезке функций с равномерной метрикой является полным метрическим пространством, а потому является банаховым, если рассматривать его как нормированное линейное пространсво.

Источник

Понятие фундаментальной последовательности.

Понятие фундаментальной последовательности.

Последовательность < > называется фундаментальной, если для любого ε>0 найдется номер N(ε) такой, что при n≥ N(ε) и для любого натурального ряда p(p=1,2,3…) выполняется неравенство 0, и воспользуемся следствием1 из теоремы23. В соответствии с этим следствием интервал интервал ( — ε, ε) содержит все элементы последовательности, начиная с некоторого номера, т.е. этот интервал содержит бесконечно много элементов последовательности < >. Т.к. , то этот интервал запишем в виде: (a- ε, ε). Этот интервал есть ε-окрестность точки a. он содержит бесконечно много элементов последовательности < >. Тогда в соответствии с 1-м определением предельной точки, число а является предельной точкой этой последовательности. Т.к. то последовательность < >. Является сходящейся.

Критерий Коши сходимости числовой последовательности(теорема25).

Для того, чтобы последовательность < > сходилась, необходимо и достаточно, чтобы она была фундаментальна.

Необходимость-считается, что последовательность < > сходится. Надо доказать, что она является фундаментальной. По определению сход. последовательности для любого ε найдется N(ε) такой, что n, поэтому при n≥ N(ε) выполняется неравенство ε , тогда по теореме24 фундаментальная последовательность является сходящейся.

Понятие производной функции, ее геометрический смысл.

Производной функции y’(x), f’(x) называетсяпредельное значение приращения функции к приращению аргумента

Геометрический смысл-tg угла наклона касательной к графику функции.

Правая и левая производные.

Правой(левой) производной функции y=f(x) называется правое(левое) предельное значение отношения приращения функции

F’(x+0) правая производная, F’(x-0) левая производная.

Дифференцируемость функции(определение. Теорема26).

Функция называется дифференцируемой в т. X, если ее приращение Δy ( в этой точке), соответствующее приращению аргумента Δx, равно Δy=A* Δx+o(Δx) не зависит от Δx.

Для того, чтобы функция была дифференцируемой в точке x₀ необходимо и достаточно, чтобы она имела этой точке конечную производную.

Необходимость-считается, что функция дифференцируема в точке x0. Надо доказать, что она имеет в этой точке производную. По определению дифференциала функции Δy= => =A+ , =A+ =A, y’(x0)=A. Δy0=y’(x0)+o( )

Достаточность-считается,что в т. x0 существует конечная производная. Надо доказать, что в x0 функция дифференцируема. По определению производной =f’(x), тогда – y’(x0)=α( = α( , =y’(x0)* +o(x)

Дифференциал функции.

Дифференциалом функции dy в точке x₀ называется главное приращение функции в этой точке dy=y’(x)*dx

Правила дифференцирования суммы, разности, произведения частного(теорема27).

Пусть функции u(x) и g(x) дифференцируемы в точке x. Тогда сумма, разность, произведение, частное(при условии, что знаменатель ≠0 в точке x) этих функций также дифференцируемы. При этом справедливы формулы:

1. .

2. .

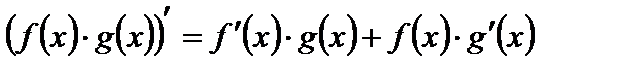
3. .

Формула Лейбница.

Y=u(x)*v(x). (uv) (n) =

Дифференциал высшего порядка. Пусть функция y=f(x) дифференцируема в точке x. dy=f’(x)dx. Если функция f’(x) дифференцируема, то можно записать d(dy)=d 2 y=d(f’(x)dx)=d(f’(x)dx=f’’(x)dxdx=f’’(x)(dx) 2

Если функция n-раз дифференцируема, то можно записать d n y=f ( n ) (x)(dx) n =f ( n ) (x)=

Дифференцирование функции, заданной параметрически. ,

Правило Лопиталя(теорема30).Пусть функция f(x) и g(x) определены и дифференцируемы в некоторой окрестности точки x₀, пусть кроме того, = =0, = =∞ и производная g’(x) отлична от 0 в рассматриваемой окрестности. Тогда если существует предельное значение , то существует и предельное значение и справедливо равенство: = . Замечание-если условие теоремы выполняется для f’(x) и g’(x), то справедливо =…… . Данное правило используется для раскрытия неопределенностей вида , , .

Формула Тейлора(теорема31).

Пусть функция у=f(x) дифференцируема n-раз в точке x₀ и некоторой окрестности этой точки. Тогда для любой точки x из этой окрестности справедлива формула:

f(x)=f(x0)+ + +…+ + , остаточное слагаемое.

В форме Пеана o((x-x0)’), в форме Лагранжа * .

Частный вид формулы Тейлора при x0 носит название формулы Маклорена.

Теорема 34.

Пусть функция y=f(x)имеет локальный экстремум в точке и дифференцируема в этой точке. Тогда f’( )=0.

Понятие фундаментальной последовательности.

Последовательность < > называется фундаментальной, если для любого ε>0 найдется номер N(ε) такой, что при n≥ N(ε) и для любого натурального ряда p(p=1,2,3…) выполняется неравенство 0, и воспользуемся следствием1 из теоремы23. В соответствии с этим следствием интервал интервал ( — ε, ε) содержит все элементы последовательности, начиная с некоторого номера, т.е. этот интервал содержит бесконечно много элементов последовательности < >. Т.к. , то этот интервал запишем в виде: (a- ε, ε). Этот интервал есть ε-окрестность точки a. он содержит бесконечно много элементов последовательности < >. Тогда в соответствии с 1-м определением предельной точки, число а является предельной точкой этой последовательности. Т.к. то последовательность < >. Является сходящейся.

Критерий Коши сходимости числовой последовательности(теорема25).

Для того, чтобы последовательность < > сходилась, необходимо и достаточно, чтобы она была фундаментальна.

Необходимость-считается, что последовательность < > сходится. Надо доказать, что она является фундаментальной. По определению сход. последовательности для любого ε найдется N(ε) такой, что n, поэтому при n≥ N(ε) выполняется неравенство ε , тогда по теореме24 фундаментальная последовательность является сходящейся.

Источник

Фундаментальная последовательность/критерий Коши

Форму привет, в Демидовиче нашел пример, не мог его решить. нашел решение в интернете и Антидемидовиче
Пример в фото, так вот, я никак не пойму, как последовательность резко превратилась в то,что выделено красным квадратом

И эта замена может использоваться только как верхняя оценка, что бы потом по двум милиционерам доказать?

Доказать, что последовательность фундаментальная
Здравствуйте! Люди добрые, помогите пожалуйста разобраться с задачами по функциональному анализу.

критерий Коши
помогите, пожалуйста, доказать фундаментальность за критерием Коши вот такой последовательности.

Критерий Коши сходимости ряда
Помогите понять критерий Коши, пожалуйста) Теорема: Для того, чтобы ряд \sum_^ <\infty>u_n.

Пределы последовательности, сходимость, критерий Коши
Помогите пожалуйста решить или понятно объясните как решать! Ни как не могу в этом разобраться(.

Решение

jogano, огромное спасибо

Добавлено через 32 минуты

Логика математика несравненна, но я в 8-м классе, просто хожу на факультатив по матану. Так вот, там как раз это обсуждали, учитель математики, тот что обычный, ужасен, не вдохновляет заниматься предметом.
А тот что ведет внеурочные занятия (в этой же школе) просто бог. Я никогда не думал, что обучение чему-то будет мотивированней чем игра в компьютер или прокрастинация. Мне уже хочется учить учить и учить и жаль что раньше учили пинками!

Т.е. для любого m поставить до фиксирования номера?

Источник